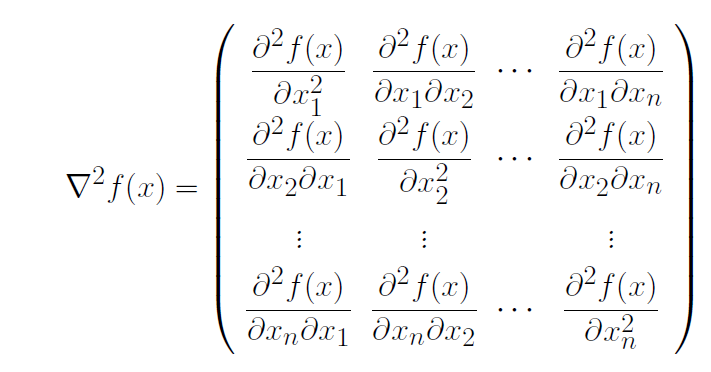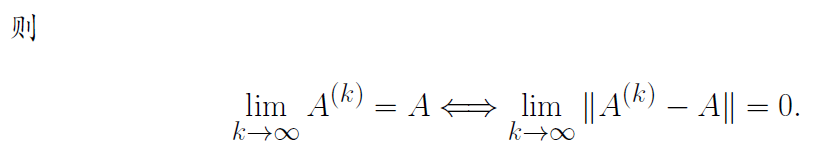1.最速下降法

鉴于自己非数学专业，数学知识薄弱，所以只写了一部分，没办法。我是先看最速下降法然后再写其他内容的，所以弃更的部分在中间。如果想接着看下去，请看书。
最优化系列会对常见的优化算法进行学习。
第一个优化算法是最速下降法，它是最优化中求解无约束优化问题的一种方法，本博客会介绍问题的简介，步骤，程序实现，程序使用，详细内容见参考文献。

说明

本文中公式编号是从1开始编号，和参考文献列举的书中公式编号无关。但是定理、算法、程序、例子等，便于使用脚注，且为了查阅方便，故采用书中的编号，且脚注上会标明是哪本书的编号。

不理解的用这个色彩表示

最优化的概念

最速下降法其中的一步会使用到线搜法，因此首先介绍线搜法。

通俗地说，所谓最优化问题，就是求一个多元函数在某个给定集合上的极值. 几乎所有类型的最优化问题都可以用下面的数学模型来描述:

min f(x),s.t. x\in K

这里，$ 𝐾 $ 是某个给定的集合(称为可行集或可行域)，$ 𝑓(𝑥) $ 是定义在集合$ 𝐾 $ 上的实值函数. 此外，在公式(1) 中，$ 𝑥 $ 通常称为决策变量, $ s.t. $ 是 subject to (受限于) 的缩写.

人们通常按照可行集的性质对最优化问题(1) 进行一个大致的分类:

线性规划和非线性规划. — 可行集是有限维空间中的一个子集;
组合优化或网络规划. — 可行集中的元素是有限的;
动态规划. — 可行集是一个依赖时间的决策序列;
最优控制. — 可行集是无穷维空间中的一个连续子集.

非线性规划

min f(x)

\begin{aligned} &\begin{array}{ll} {\text { s.t. }} & {h_{i}(x)=0, i=1, \cdots, l} \\ {} & {g_{i}(x) \geq 0, \quad i=1, \cdots, m} \end{array} \end{aligned}

其中， $𝑓(𝑥), ℎ_𝑖(𝑥) (𝑖 = 1, · · · , 𝑙)$ 及 $𝑔_𝑖(𝑥) (𝑖 = 1, · · · ,𝑚)$ 都是定义在 $R_𝑛$ 上连续可微的多元实值函数,且至少有一个是非线性的.记 $𝐸={𝑖:ℎ_𝑖(𝑥)=0},𝐼={𝑖:𝑔_𝑖(𝑥)≥0}.$ 若指标集 $𝐸∪𝐼=∅$ 称之为无约束优化问题，否则称为约束优化问题.特别地,把 $𝐸 \neq ∅$ 且 $𝐼=∅$ 的优化问题称为等式约束优化问题;而把 $𝐼 \neq ∅$ 且 $𝐸 = ∅$ 的优化问题称为不等式约束优化问题. $𝑓(𝑥)$ 称为目标函数, $ℎ_𝑖(𝑥),𝑔_𝑗(𝑥)(𝑖=1,···,𝑙;𝑗=1,···,𝑚)$ 称为约束函数.此外，通常把目标函数为二次函数而约束函数都是线性函数的优化问题称为二次规划；而目标函数和约束函数都是线性函数的优化问题称为线性规划.

向量范数

在算法的收敛性分析中，需要用到向量和矩阵范数的概念及其有关理论.

设 $\mathbb{R}^n$ 表示实𝑛维向量空间， $\mathbb{R}^{𝑛×𝑛}$ 表示实𝑛阶矩阵全体所组成的线性空间.在这两个空间中，我们分别定义向量和矩阵的范数.

向量范数的定义

\left \|x\right\|_p=({\sum_{i=1}^n{\left|x\right|^p}})^{\frac{1}{p}}

常用的范数:

1范数元素绝对值之和

\left \|x\right\|_1={\sum_{i=1}^n{\left|x\right|}}

2范数元素的平方和开根号

\left \|x\right\|_2=\sqrt{\sum_{i=1}^n{\left|x\right|}^2}

无穷范数元素绝对值的最大值

\left \|x\right\|_\infty=\max_{1\leq i\leq n} \left|x_i\right|

向量范数的性质

非负性 $\left \|x\right\| \geq 0$ $\left \|x\right\|=0 \Longleftrightarrow x=0$
齐次性 $\left \|\lambda x\right\|=\left|\lambda\right|\left \|x\right\|,\lambda\in\R$
三角不等式 $\left\|x+y\right\|\leq\left \|x\right\|+\left \|y\right\|$

矩阵范数

矩阵范数的性质

矩阵范数的定义和性质与向量范数一致。除此之外，还有以下两条性质

柯西不等式 $\left \|AB\right\|\leq\left \|A\right\| \bullet \left \|B\right\|,A,B\in \mathbb{R}^{n \times n}$

矩阵范数和向量范数的联系

相容性 $\left \|Ax\right\|\leq\left \|A\right\|_\mu\left \|x\right\|,x\in\mathbb{R}^n,A\in \mathbb{R}^{n\times n}$
矩阵范数和向量范数是相容的，怎么理解
算子范数:，若存在 $x\neq 0$ ，且
$\|A\|_{\mu}=\max _{x \neq 0} \frac{\|A x\|}{\|x\|}=\max _{\|x\|=1}\|A x\|, \quad A \in \mathbb{R}^{n \times n}$

则称矩阵范数 $\|\bull\|_{\mu}$ 是由向量范数 $\|\bull\|$ 诱导出来的算子范数，简称算子范数，有时也称为从属于向量范数 $\|\bull\|$ 的矩阵范数. 此时向量范数和算子范数通常采用相同的符号 $\|\bull\|$ 。

常见的诱导范数

从属于向量范数 $\|x\|_\infty$ , $\|x\|_1$ , $\|x\|_2$ 的矩阵范数分行和范数、列和范数和谱范数。

\|A\|_{\infty}=\max _{1 \leq i \leq n} \sum_{j=1}^{n}\left|a_{i j}\right|

\|A\|_{1}=\max _{1 \leq j \leq n} \sum_{i=1}^{n}\left|a_{i j}\right|

\|A\|_{2}=\max \left\{\sqrt{\lambda} | \lambda \in \lambda\left(A^{T} A\right)\right\}

行和范数，即所有矩阵行向量绝对值之和的最大值。列和范数，即所有矩阵列向量绝对值之和的最大值。谱范数，即 $A^TA$ 矩阵的最大特征值的开平方(开平方即为开根号的意思)。

常见的非诱导范数

非诱导范数常见的为 F - 范数，即 Frobenius 范数以及核范数。

Frobenius 范数，即矩阵元素绝对值的平方和再开平方。

\|A\|_{F}=\left(\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j}^{2}\right)^{1 / 2}=\sqrt{\operatorname{tr}\left(A^{T} A\right)}

核范数^[1] Nuclear Norm，即矩阵奇异值的和^[1:1]。

\|A\|_{*}=\sum_{i=1}^{n} \lambda_{i},\lambda_i为矩阵A的奇异值

向量序列和矩阵序列的收敛性

向量序列和矩阵序列的收敛性^[2]

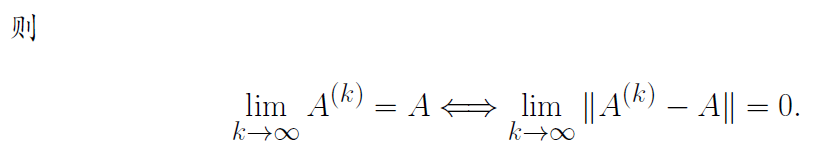
收敛性暂时不做考虑，这一节仅列举出来供参考。

函数的可微性

本节主要介绍后文经常需要用到 $𝑛$ 元函数的一阶和二阶导数以及泰
勒展开式.

定义1.1

设有 $𝑛$ 元实函数 $𝑓(𝑥),$ 其中自变量 $𝑥 = (𝑥_1, · · · , 𝑥_𝑛)^𝑇 ∈R_𝑛$ 称向量

\nabla f(x)=\left(\frac{\partial f(x)}{\partial x_{1}}, \frac{\partial f(x)}{\partial x_{2}}, \cdots, \frac{\partial f(x)}{\partial x_{n}}\right)^{T}

为 $f(x)$ 在 $x$ 处的一阶导数或梯度。

称矩阵

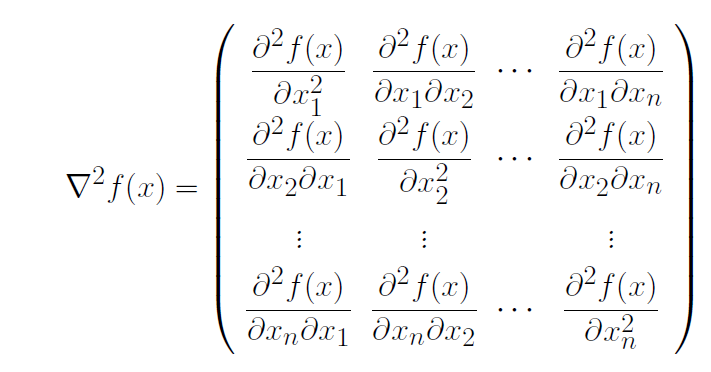
为 $f(x)$ 在 $x$ 处的二阶导数或Hesse矩阵。若梯度 $∇𝑓(𝑥)$ 的每个分量函数在 $𝑥$ 都连续, 则称 $𝑓$ 在 $𝑥$ 一阶连续可微；若Hesse 阵 $∇^2𝑓(𝑥)$ 的各个分量函数都连续，则称 $𝑓$ 在 $𝑥$ 二阶连续可微.

若 $𝑓$ 在开集 $𝐷$ 的每一点都连续可微，则称 $𝑓$ 在 $𝐷$ 上一阶连续可微；若 $𝑓$ 在开集 $𝐷$ 的每一点都都二阶连续可微，则称 $𝑓$ 在 $𝐷$ 上二阶连续可微.

函数的泰勒展开

弃更了，准备先看看再更新这个内容吧，我太难了。

最速下降法

多维无约束优化问题是指在没有任何限制条件下寻求目标函数的极小点，其表达多维无约束优化问题是指在没有任何限制条件下寻求目标函数的极小点，其表达式为

\min _{x \in \mathbb{R}^{n}} f(x)

问题简介

最速下降法由法国数学家 Cauchy于1947年首先提出。该算法在每次迭代中，沿最速下降方向（负梯度方向）进行搜索，每步沿负梯度方向取最优步长，因此这种方法也称为最优梯度法。

最速下降法方法简单，只以一阶梯度的信息确定下一步的搜索方向，收敛速度慢；越是接近极值点，收敛越慢；它是其他许多无约束、有约束最优化方法的基础。该方法一般用于最优化开始的几步搜索。^[3]

问题步骤

最速下降法是用负梯度方向

d_{k}=-\nabla f\left(x_{k}\right)

作为搜索方向的，因此也称为梯度法。

解释如下：

设 $f(x)$ 在 $x_k$ 附近连续可微， $d_k$ 为搜索方向向量， $g_{k}=\nabla f\left(x_{k}\right)$ . 由泰勒展开式得：

f\left(x_{k}+\alpha d_{k}\right)=f\left(x_{k}\right)+\alpha g_{k}^{T} d_{k}+o(\alpha), \quad \alpha>0

那么目标函数 $f(x)$ 在 $x_k$ 处沿方向 $d_k$ 下降的变化率为

\begin{aligned} \lim _{\alpha \rightarrow 0} \frac{f\left(x_{k}+\alpha d_{k}\right)-f\left(x_{k}\right)}{\alpha} &=\lim _{\alpha \rightarrow 0} \frac{| \alpha g_{k}^{T} d_{k}+o(\alpha)}{\alpha} \\ &=g_{k}^{T} d_{k}=\left\|g_{k}\right\|\left\|d_{k}\right\| \cos \bar{\theta}_{k} \end{aligned}

其中 $\bar\theta_k$ 是 $g_k$ 和 $d_k$ 的夹角。显然，对于不同方向 $d_k$ ，函数变化率取决于它与 $g_k$ 的夹角的余弦值。要想使变化率最小，只有 $cos(\bar\theta_k)=-1$ ，即 $\bar\theta_k=\pi$ 时才能达到，亦即 $d_k$ 应该取(2)中的负梯度方向，这也是将负梯度方向叫做最速下降方向的由来。下面给出最速下降法的具体计算步骤。

算法3.1 最速下降法^[2:1]

步0 选取初始点 $x_{0} \in \mathbb{R}^{n}$ ，容许误差 $0 \leq \varepsilon \ll 1$ .令k:=1.

步1 计算 $g_k=\Delta f(x_k)$ .若 $\left\|g_{k}\right\| \leq \varepsilon$ ，停算，输出 $x_k$ 作为近似最优解。

步2 取方向 $d_k=-g_k$

步3 由线搜索技术确定步长因子 $\alpha_k$ .

步4 令 $x_k+1:=x_k+\alpha_k d_k$ ， $k=k+1$ ，转步1

说明步3中步长因子 $α_k$ 的确定即可使用精确线搜索方法，也可以使用非精确线搜索方法，在理论上都能保证其全局收敛性。

精确线搜索方法保证全局收敛性的证明如下：

若采用精确线搜索方法，即

f\left(x_{k}+\alpha_{k} d_{k}\right)=\min _{\alpha \geq 0} f\left(x_{k}+\alpha d_{k}\right)

那么 $\alpha_k$ 应满足

\phi^{\prime}(\alpha)=\left.\frac{\mathrm{d}}{\mathrm{d} \alpha} f\left(x_{k}+\alpha d_{k}\right)\right|_{\alpha=\alpha_{k}}=\nabla f\left(x_{k}+\alpha_{k} d_{k}\right)^{T} d_{k}=0

由(2)式有

\nabla f\left(x_{k+1}\right)^{T} \nabla f\left(x_{k}\right)=0

即新点 $x_{k+1}$ 处的梯度与旧点 $x_k$ 处的梯度是正交的，也就是说迭代点列所走的路线是锯齿型的，故其收敛速度是很缓慢的(至多线性收敛速度)。

由 $d_k=-g_k$ 及下式

\cos \theta_{k}=\frac{-g_{k}^{T} d_{k}}{\left\|g_{k}\right\|\left\|d_{k}\right\|}=\frac{-g_{k}^{T}\left(-g_{k}\right)}{\left\|g_{k}\right\|\left\|-g_{k}\right\|}=1, \Rightarrow \theta_{k}=0

故条件 $0 \leq \theta_{k} \leq \frac{\pi}{2}-\mu, \quad \mu \in\left(0, \frac{\pi}{2}\right)$ 。从而直接应用定理2.2^[2:2]和定理2.3^[2:3]即得最速下降法的全局收敛性定理。

最速下降法全局收敛性定理3.1：

设目标函数 $f(x)$ 连续可微且其梯度函数 $\Delta f(x)$ 是Lipschitz连续的， $\{x_k\}$ 由最速下降法产生，其中步长因子 $\alpha_k$ 由精确线搜索或由Wolfe 准则, 或由Armijo 准则产生。则有
$\lim _{k \rightarrow \infty}\left\|\nabla f\left(x_{k}\right)\right\|=0$

程序实现

下面给出基于Armijo 非精确线搜索的最速下降法Matlab 程序.

程序 3.1(最速下降法)

function [x,val,k]=grad(fun,gfun,x0)
% 功能: 用最速下降法求解无约束问题:  min f(x)
%输入:  x0是初始点, fun, gfun分别是目标函数和梯度
%输出:  x, val分别是近似最优点和最优值,  k是迭代次数.
maxk=5000;   %最大迭代次数
rho=0.5;sigma=0.4;
k=0;  epsilon=1e-5;
while(k<maxk)
    g=feval(gfun,x0);  %计算梯度
    d=-g;    %计算搜索方向
    if(norm(d)<epsilon), break; end
    m=0; mk=0;
    while(m<20)   %Armijo搜索
        if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)
            mk=m; break;
        end
        m=m+1;
    end
    x0=x0+rho^mk*d;
    k=k+1;
end
x=x0;
val=feval(fun,x0);

程序使用

例3.1 利用程序3.1求解无约束优化问题

\min _{x \in \mathbb{R}^{2}} f(x)=100\left(x_{1}^{2}-x_{2}\right)^{2}+\left(x_{1}-1\right)^{2}

该问题有精确解 $x^*=(1,1)^T,f(x^*)=0$ 。

分别建立grad.m(1.3 程序实现)，fun.m，gfun.m脚本函数。

%计算目标函数
function f=fun(x)
f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;

% 计算目标函数的梯度
function g=gfun(x)
g=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1), -200*(x(1)^2-x(2))]';

main函数如下，用于调用上述函数。

%main函数
x0_set=[0,0;2,1;1,-1;-1,-1;-1.2,1;10,-10];
for i_x0=1:size(x0_set,1)
    x0=x0_set(i_x0,:)';
    [x,val,k]=grad('fun','gfun',x0);
    %x0是初值，x是最小值，f(x)是最小函数值,nitr是迭代次数
    fprintf('x0:(%.2f,%.2f) x:(%.2f,%.2f) y:%f nitr:%d\n',x0(1),x0(2),x(1),x(2),val,k); 
end

选取初值 $x0$ 为不同的值，有不同的结果。运行结果如下：

参考文献^[4]

[矩阵范数及其求导](https://www.cnblogs.com/go-go/p/9674984.html) ↩︎ ↩︎
马昌凤. 最优化方法及其Matlab程序设计[M]. 科学出版社, 2010. ↩︎ ↩︎ ↩︎ ↩︎
李娅. MATLAB R2015b最优化计算[M]. 清华大学出版社, 2017. ↩︎
参考文献格式：中华人民共和国国家标准GBT7714-2015 ↩︎

说明